Position, Velocity, and Acceleration of Vector Functions

 

Introduction

   When dealing with projectiles in physics and/or calculus, it is often necessary to decide the object's position, velocity, and acceleration. For a basic understanding of speed, velocity, and acceleration, please visit http://www.sparknotes.com/testprep/books/sat2/physics/chapter5section2.rhtml , as this study will cover the more complex calculus concepts of position, velocity, and acceleration in the form of vectors.  Position (often notated as x(t)) shows a projectile's location with respect to a starting location, and is always denoted with a unit of distance, such as meters or feet. In an x-y plane, position shows how far an object has moved (y) in a given amount of time (x). Please visit http://www.physicsclassroom.com/class/vectors/ for more information regarding vectors in a 2D plane. In this example, we will use the position function y=x³+1. This function and its graph below show how far the projectile has traveled (y) in a given amount of time (x):

 

*note tilt your head to the right while looking at the graph*

http://img690.imageshack.us/i/assignments005.jpg/

 

 

 

   At x=1 second, the projectile is at 2 meters.

 

   The rate of change of position (the derivative of the position function) is velocity. Velocity shows how fast position changes and is measured in some unit of speed (in this case, meters/second). Graphically, the slope, or derivative, of the position vs. time graph is the velocity vs. time graph. Slope in the Cartesian coordinate plane is equal to the change in y divided by the change in x. Here, the change in y is the change in position and the change in x is the change in time. Velocity, therefore is equal to the change in position over a given time interval, or meters per second in our example.

   When velocity is not equal to zero, position must be changing. The rate of change of the position function at any point on the graph of position vs. time can be found by looking at the corresponding point on the graph of velocity vs. time. This velocity graph can be found by graphing the derivative of the position function. In this case, the velocity equation would be y=3x², the derivative of the position function:

 

*note tilt your head to the right while looking at the graph*

http://img508.imageshack.us/i/assignments006.jpg/

 

 

   At a time of x=1 second, the particle is at 2 meters (according to the position function) going 3 meters/second (according to the velocity function).

 

   The rate of change of velocity is acceleration. Acceleration relates to how fast velocity changes over a given time interval and is measured in velocity divided by time. Since meters/second is being used for velocity in this example, velocity would be (m/s)/s, or velocity/time. Acceleration, being the rate of change of velocity, can be found by taking the derivative of the velocity equation. The resulting equation (acceleration vs. time) can then be graphed. Each point on the acceleration vs. time graph shows how much the projectile is accelerating at each point in time. In our example, the acceleration function would be y=6x, the derivative of the velocity function:

 

*note tilt your head to the right while looking at the graph*

http://img854.imageshack.us/i/assignments007.jpg/

 

 

   At a time of x=1 second, the particle  is at 2 meters (according to the position function) going 3 meters/second (according to the velocity function) and accelerating at a rate of 6 m/s/s (according to the acceleration function).

 

 

Moving Between Position, Velocity, and Acceleration

   As previously mentioned, the velocity function can be found by taking the derivative of the position function, and the acceleration function can be found by taking the derivative of the velocity function. Graphically, this is because the slope of a position function (or ratio of position to time) is velocity, and the slope of velocity (or ratio of velocity to time) is acceleration. This graphical analysis is further shown in the image below. In other words, meters show position, meters divided by time shows velocity, and (meters divided by time) divided by time shows acceleration. 

 

 

   Conversely, if this process is reversed, velocity can be found from acceleration, and position can be found from velocity. Instead of taking the derivative of each equation, we would instead find the integral. Graphically, instead of taking the slope of each curve, we are finding the area under each curve, or the y value of each equation (acceleration and velocity) multiplied by the x value (time). In other words (m/s/s)x(s)=(m/s), and (m/s)x(s)=(m).

 

A Vector Approach 

  In more advanced mathematics, the motion of a projectile is examined not only in a single dimension, but as movement in three dimensions. To measure such position, the variable system is rearranged. X now shows movement in the right/left direction, Y now shows movement in the up/down direction, and Z now shows movement in the in/out direction. Each of these directions are now put in terms of T (the amount of time for the projectile). Instead of functions in the form x-y or x-y-z, now functions are made for each direction, each with the dependent variable t for time. As a result, each direction is parameterized into separate functions: x(t), y(t), and z(t). 

 

  These functions can then be combined into one single form, called vector form. Vectors are combinations of the three direction equations, all dependent on time (t). They are expressed as:

 

x(t)i+y(t)j+z(t)k

 

  Vectors can be used to portray more complicated paths as they can show movement in three dimensions:

 

 

  Vectors in general are instrumental to the study of calculus and physics concepts, as they provide a concrete mathematical framework to better understand a particle or object's position, velocity, speed, and acceleration with respect to time and space. This study will focus specifically on position, velocity, and acceleration vectors. Please visit http://www.ltcconline.net/greenl/courses/202/vectorFunctions/velacc.htm to learn more about the applications of vectors, which include everything from charting spaceflight to countering an enemy missile attack. 

 

Part I: The Position Vector

  A position vector is a vector that extends from a specific reference point to the actual position of the particle.

 

 

In this case, the vector r is extending from O (the origin) to point P (x,y).

 

The position vector is always based on the origin of the coordinate system. Due to this fundamental attribute of vectors, scalar components of these vectors occur in three perpendicular directions and are equal to the coordinates. The scalar components of this vector (denoted as r) in the direction of these perpendicular line segments are: 

x=rcosα

y=rcosβ

z=rcosγ

(see image below)

 

 

This position vector in terms of (x,y,z) coordinates is:

 

r = xi + yj + zk

 

i is the unit vector along the x axis, j is the unit vector along the y axis, and k is the unit vector along the z axis.

    *On a side note, the magnitude of a position vector is found by manipulating the formula r=|r|=((x^2)+(y^2)+(z^2)) ^ (1/2)

 

Part II: The Velocity Vector

 

 

A velocity vector is a vector that measures the rate of change of the position vector. Consider the position vector   r = (3t^3+6)i + (17−8t^2)j + (−t^4)k

To find the rate of change of the position function (the velocity vector), take the derivative of each portion of the position vector. Thus, r' = (9t^2)i + (−16t)j + (−4t^3)k. A visual of the velocity vector in motion compared with the position vector is shown below.

 

 

 

 

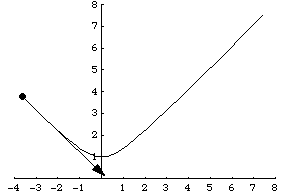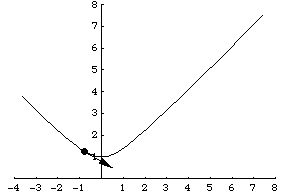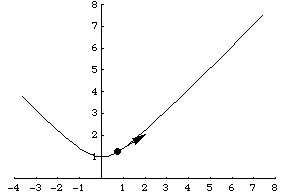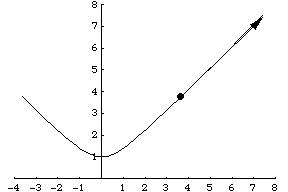
Part III: The Acceleration Vector

 

An acceleration vector is a vector that measures the rate of change of the velocity vector. Consider the previous velocity vector r' = (9t^2)i + (−16t)j + (−4t^3)k. To find the acceleration vector, one must again take the derivative of each component. Thus, the acceleration vector is r'' = (18t)i −16j + (−12t^2). The image above has the same basic concept, and illustrates the acceleration vector with respect to the velocity vector. 

 

Switching between position, velocity, and acceleration with vectors requires the same process as with the x-y coordinate plane. Switching from position to velocity and from velocity to acceleration still requires differentiation, and switching from acceleration to velocity and from velocity to position still requires integration. 

 

Differentiation and integration of vectors involve simply differentiating and integrating each vector component:

 

If r(t)=x(t)i+y(t)j+z(t)k, then

r'(t)=x'(t)i+y'(t)j+z'(t)k

 

 

---

 

Tangential and Normal Components of Acceleration

 

When we’re working in one dimension, the effects of acceleration are fairly easy to calculate, as it can cause velocity to either increase or decrease. This is not the case when we scale up to two dimensions, because acceleration can now move velocity up, down, left, right, or a combination of any two non-opposing directions. Due to this increased difficulty, it is often much easier to see the effects of acceleration on velocity if we have a component of acceleration that moves in the direction of the curve and a component of acceleration that moves in a perpendicular direction to the curve. These two components are called the tangent component of acceleration and the normal component of acceleration, respectively.

 

Once we know this, an obvious question arises: how do we calculate each. Well, the first step is to analyze what we need, which is the direction tangent to the curve, the direction normal to the curve, the magnitude of the acceleration vector devoted to the tangent direction and the magnitude devoted to the normal direction.

 

The easiest one to find is the direction tangent to the velocity vector. A direction is described using a unit vector, and so the tangent direction can be found using the unit tangent vector, the equation of which is as follows:

 

 

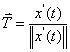
The direction tangent to the curve r is therefore

 

 

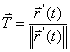
Manipulating the equation we have this:

 

 

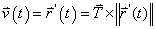
Since acceleration is the derivative of velocity, we can take the derivative of the previous equation using the product rule.

 

 

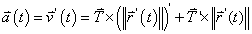
The first part of the acceleration is tangent to the curve, as the direction is defined using the unit tangent vector. By proof #4, the second part of the acceleration is normal to the curve. We now have all four of our necessary items and can formulate the tangent and normal components of acceleration by simplifying either part of the above equation.

 

Note that if one component is already calculated, the other can be more easily calculated by subtracting the first from the acceleration vector. 

 

Real World Applications (and some physics)

Common applications of position, velocity, and acceleration functions include 3 types of projectile motion. With regards to all types of projectiles and just forces in general is the equation Force = Mass X acceleration. The first type of projectile is dropping/throwing objects off of buildings otherwise known as a type 1 projectile.  The position function follows the following format:

+\-4.9t² +/- (initial acceleration)t +/- (the height of the building) for problems dealing in meters
+\- 16t² +/- (initial acceleration)t +/- (the height of the building) for problems dealing in feet

 

Vectors can also be applied when dealing with other types of projectile motion such as when an object is shot from the ground into the air (also known as a type 2 projectile):

(insert picture here when I figure it out)

Key questions that can be asked involving type II projectiles are the max height, flight time, and range. The equation for max height the equation for which equals the initial velocity times the sine of the angle it is shot into the air squared over twice the value of gravity

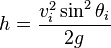
The range is the same equation except twice angle and doubled.

Type III projectiles include combining Type I and Type II. They are objects shot from an elevation above the ground. They compile properties of both.

 

                     

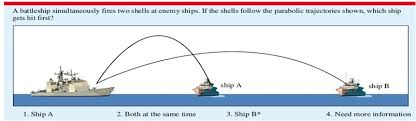
Proofs

The proofs that follow feature vectors that have a specific number of terms, but they can be generalized to any number of terms.

 

Proof #1

To be proven: Vectors are derived component-wise. In other words, if

 

 

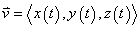
then

 

 

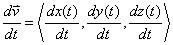
Proof:

The limit of a vector is defined as the limit of its components, so

 

 

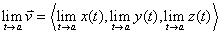
The definition of the derivative is as follows:

 

 

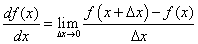
If the definition of the derivative is applied to vectors, we get this:

 

 

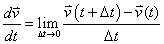
Using the basic properties of vectors that allow us to sum and subtract component-wise and to divide a vector by a scalar, we can do this:

 

 

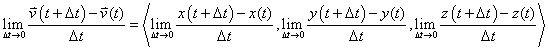
By applying the definition of the derivative, we reach this conclusion:

 

 

Therefore,

 

 

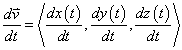
Q.E.D.

 

Proof #2

To be proven: Vectors are integrated component-wise. In other words, if

 

 

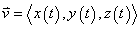
then

 

 

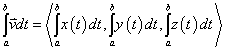
Proof:

 

 

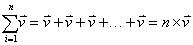
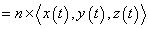
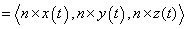
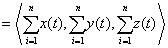
The definition of a definite integral using Riemann sums is as follows:

 

 

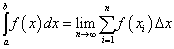
Using the definition on a vector, we can surmise

 

 

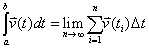
We previously proved that

 

 

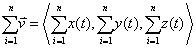
Using that and the property of vectors that allows a component-wise solution of limits, we get this:

 

 

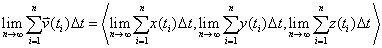
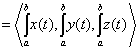
Therefore,

 

 

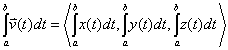
Q.E.D.

 

Proof #3

To be proven: The derivative of a dot product follows pattern set by the product rule. In other words,

 

 

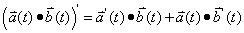
Proof:

Let

 

 

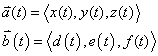
If we allow those definitions,

 

 

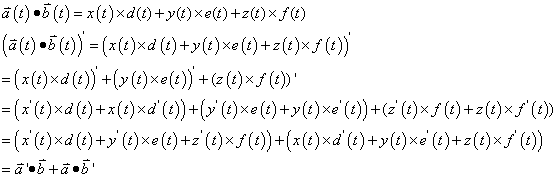
Therefore,

 

 

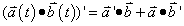
Q.E.D.

 

Proof #4

To be proven: The derivative of the unit tangent vector is perpendicular to it. In other words,

 

 

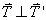
Proof:

Let v be a non-constant vector that has a constant length.

 

 

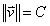
The dot product of any vector and itself is its length squared, so

 

 

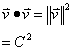
Since the dot product of v and itself is a constant, the derivative of the dot product is zero.

 

 

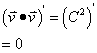
By proof #3, we can simplify the derivative of the dot product like so:

 

 

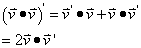
Since v dotted with its derivative is zero, we can conclude that v is perpendicular to its derivative.

The unit tangent vector has a constant length, so it is perpendicular to its derivative.

Q.E.D.

 

Proof #5

 

To be proven:

                                                      

 

Proof:

I have discovered a truly marvelous proof of this, which this web-page unfortunately has too small a storage capacity to contain.

 

Extra Practice

 

Example 1:

Find the velocity vector v(t) if the position vector is 

        r(t)  =  3ti + 2t²j - sin t k 

 

Example 2:

Let 

        r(t)  = 3i + 2t j + cos t k

Find the speed after p/4 seconds. 

 

 

Example 3:

Find the velocity and acceleration of the position function

        r(t)  = (2t - 2) i + (t² + t + 1)j 

when t  =  -1.  Then sketch the vectors.

 

 

 

Solution 1:

We just take the derivative

        v(t)  =  3i + 4tj + cos t k 

Solution 2:

We first find the velocity vector

        v(t)  =  r'(t)  =  2 j - sin t k

We have 

        v(p/4)  =  2 j - 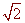/2 k

Its magnitude is the square root of the sum of the squares or

        Speed  =  || v ||  =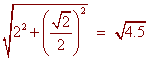 

 

Solution 3

The velocity vector is

        v(t)  =  r'(t)  =  2i  + (2t + 1) j

Plugging in -1 for t gives

        v(-1)  =  2i - j

Take another derivative to find the acceleration.

        a(t)  =  v'(t)  =  2j

 

Example 4:

Luke Skywalker's X-Wing is approaching the Death Star. Up until this point, his ship, as well as every other ship in the Rebel fleet was travelling at 900 ft/s at an angle of 45 degrees above the horizontal. However, at t=0 minutes, Gold Leader signals all ships to move into attack position. If Luke continues at the same velocity, he will surely be shot down by one of the enemy fighters on his tail. Knowing that this would prematurely end the Star Wars series, Luke realizes that he cannot let this happen, and accelerates according to the vector:

a(t)=-32j

A leading imperial star destroyer will be at the position of Luke's maximum possible height. Luke realizes that R2 is annoying beyond any description, and the only way to end the droid's constant noise is to crash it into the star destroyer. The star destroyer will be at this position when t=18 minutes. Will Luke's attempt to end the annoying noise of R2-D2 be successful?

 

Solution

a(t)=-32j               Integrate

v(t)=(-32t)j+v₀         We know that v₀ is equal to 900 ft/s at 45 degrees above the horizontal. Next, divide this initial value into horizontal (i) and vertical (j) parts.        

v(t)=(-32t)j+900sin(45)j+900cos(45)i        Simplify

v(t)=900cos(45)i+(900sin(45)-32t)j           This is the velocity vector. The maximum height occurs where the vertical (j) component equals zero

0=900sin(45)-32t                                   Algebra

t= about 20 minutes 

 

No, Luke will miss the Star Destroyer by two minutes. He will therefore be stuck listening to R2-D2 for the rest of the series. To keep himself sane, Luke learns to use the force to keep R2's "mute" button pushed.

 

 

  

 

Challenge Question:

You are Chewbakka. Your monsterous roars can destroy deadly missiles launched at you. 

The position of a deadly incoming missile is defined by the vector: r= 1000i + 500j

The velocity is defined by the vector: v= -30i + 3j

 

assuming that your roar works as a projectile and the only force that acts upon it is gravity which is equal to that of earth's (9.8) what is the angle you must launch your roar to destroy the missile?

Solution:

 .625 radians 

 

Challenge Question 2:

You are Luke Skywalker and  have spotted Darth Vader in his TIE Fighter. Using your amazing vector knowledge, you recognize his movement in space as following the vector-valued function r(t)=<t^2, 7t-12, t^2>. You fire off a missile that is set to travel as s(t)=<4t-3, t^2, 5t-6> dictates. Does you missile hit Darth Vader?

 

Solution:

Yes. This can be solved by setting each part of the first vector equal to its corresponding part in the other vector.

 

x-coordinate: t^2=4t-3

t=1,3

y-coordinate: 7t-12=t^2

t=3,4

z-coordinate: t^2=5t-6

t=2,3

 

Since all of the coordinates are equal at a common t, the vectors at some point meet (in this case, t=3), which means that the missile will collide with Darth Vader.

 

Challenge Question 3:

You are Marty McFly and are attempting to make a time jump with Doc Brown's Flux Capacitor in order to avoid the dinosaurs that are chasing after you. Due to the slope of the territory that you are traversing, you cannot go straight, so your path follows r(t)=<5(t+2)^2, t+7>, but you only have enough gas to travel 400 units. The only problem other than the gas shortage is that the dinosaur chasing you follows a path of s(t)=<t^3-28t, t^2-8t-3>. Will you be caught by the dinosaur before or after running out of gas, or will you reach a speed of 88 units per hour and go return safely to your proper time?

 

Solution:

This problem has three parts: when will you reach 88 units per hours, when will you run out of gas, and when will the dinosaur catch you, if ever.

 

1. v(t)=r'(t)=<10(t+2), 1>

speed=magnitude(v(t))=sqrt(100(t+2)^2+1)

The speed is 88 at approximately t=6.7994.

 

2. Distance traveled=integral(speed,t,0,k)

If the distance traveled is set to 400 and the equation is solved for k, we find that the time at which the gas runs out is approximately 7.1643.

 

3. To find if/when the dinosaur catches us, we must set each component of the first vector equal to the corresponding component of the dinosaur's vector.

x-component: 5(t+2)^2=t^3-28t

t=10

y-component: t+7=t^2-8t-3

t=10

Since the times match, we now that the dinosaur catches up to us at t=10.

 

Luckily for us, the time at which we reach a speed of 88 is before the others, so we get away from the situation without much harm.

 

http://www.ocf.berkeley.edu/~tkle/bc/VECTORS.pdf

http://apcentral.collegeboard.com/apc/public/repository/ap07_calculus_bc_form_b_q2.pdf