INTRODUCTION

 

L'Hopital's Rule was founded by the french mathematician Guillame de L'Hopital during the late 17th century. L'Hopital published his rule in the first calculus book of derivatives, called Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes. However, some do believe that the rule was discovered by Johann Bernoulli.  

 

 

L'Hopitals rule allows us to evaluate the limit of a term or an indeterminate function. It usually converts a limit from an indetermiate form to a determinate form, enabling an easy evaluation for the limit. L'hopital's rule states that given an unresolvable limit of the form 0/0 or /, the ratio of the functions of f(x)/g(x) will have the same limit at C as the ratio of f"(x)/ g'(x). 

Therefore, the  lim  F(X) =  lim  F'(X). 

                      xc G(X)    x-> c G'(x) 

 

 

L'Hopital's rule may be applied indefinitely as long as the conditions are satisfied. However, it is important to note that the nonexistance of limf(x)/g(x) does not prove the nonexistance of limf(x)/g(x).

 

Before you start

What normally should you try first?

-Rewrite the expression using algebraic techniques like... dividing by the denominator or dividing by term with highest power in the denominator

When all else fails, use L'Hopital! 

 

Pre-requisite: 

 

The requirement that the limit

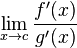
exist is essential. Differentiation of indeterminate forms can sometimes lead to limits that do not exist. If this happens, then l'Hôpital's rule does not apply.

 

 

How to use L'Hopitals Rule

Step 1: First determine if you can use L'Hopital's rule. It can only be used when you are finding the limit of two functions written as f(x) divided by g(x), and you get an indeterminate from of infinity divided by infinity, or zero divided by zero

Step 2: Take the derivatives of both the top and bottom

Step 3: Find the limit of the derivatives that you find (the answer is also the limit of the initial function)

Step 4: Repeat Steps 2 and 3 as necessary, sometimes you will get an indeterminate form after using L'Hôpital's rule the first time, so continue using it until you get a determinate value

 

Note:  Taking the individual derivatives of the denominator and numerator are essential in solving these problems. Therefore, it is necessary to know the basic derivative rules:

 

General Method For Indeterminate form:

Step 1:First we must find if as the limit approaches c the function is indeed in indeterminate form

Step 2: If it is factor the numerator and denominator

Step 3:Reduce it to its simplified form

Step 4: Plug in the constant 

 

Definition of Indeterminate form:

Answers in a form in which one cannot determine the true solution from that answer or by direct substitution. 

 

Key types of Indeterminate Form: 

 

0⁰, 0/0, 1^∞, ∞ − ∞, ∞/∞, 0 × ∞, and ∞⁰

 

Formal Definition of L'Hopital's Rule:

Let f and g be function that are differentiable on an open interval (a,b) containing c, except possibly at c itself. Assume that g'(x) does not equal 0 for all x in (a,b), except possibly at c iteslt. If the limit of f(x)/g(x) as x approaches c produces the indeterminate form 0/0, then

provided the limit on the right exists (or is infinite). This result also applies if the limit of f(x)/g(x) as x approaches c produces any one of the indeterminate forms. 

 

 WARNING: 

This rule is not to be confused with the Quotient Rule. L'Hopital takes the independent first derivatives of the top and bottom. Quotient Rule is the first derivative of the overall, united function. 

 

EXAMPLES of L'Hopital's Rule

 

EXAMPLE 1:

 

.

 

Both the top and bottom limits of the first fraction are zero, so we can use l'Hôpital's Rule and take derivatives. Note that 2x is the derivative of x^2-4, and 2x-3 is the derivative of x^2-3x+2. We can then continue to find that

 

EXAMPLE 2:

Find the limit lim_{x� 1} ( x ² - 1 ) / (x - 1)

Since the limit of the numerator=

lim_{x� 1} ( x ² - 1 ) = 0

and that of the denominator

lim_{x� 1} x - 1 = 0

are both equal to zero, we can use L'hopital's rule to calculate limit

lim_{x� 1} ( x ² - 1 ) / (x - 1) = lim_{x� 1} [ d ( x ² - 1 ) / dx ] / [ d ( x - 1 ) / dx ]

= lim_{x� 1} 2 x / 1 = 2

Note that the same limit may be calculated by first factoring as follows

lim_{x� 1} ( x ² - 1 ) / (x - 1)

= lim_{x� 1} ( x - 1 )(x + 1) / (x - 1) =

= lim_{x� 1} (x + 1) / 1 = 2

 

 

For more practice on L'Hopital's rule, use the interactive website: 

http://www.karlscalculus.org/calc8_0.html#l_rule

 

Examples of Indeterminate Form:

 Example 1: illustrates a limit being in the indeterminate form of infinity over infinity  

Lim            (x^6+x^5+3x^2)/(2x^6+4x^4+2x^3+x)

x->∞

 

 This limit is in the form of  infinity over infinity.  Therefore, if the degree in the denominator is higher than the degree in the numerator than your limit is zero. If the degrees are the same, then your answer is the coefficients of the variables with the highest degrees. If the degree on the top is bigger than the degree on the bottom, then your answer Does Not Exist (DNE). 

The answer is 1/2 in this case because the highest degrees are the same so you can just use the coefficients of the highest degree variables. L'Hopital's rule can be applied. 

 

Example 2: illustrates a limit being in the indeterminate form of infinity minus infinity

 

lim   (1 /ln (x)) − (1 /(x − 1)) =∞ − ∞  

 x→1

 

Simplifies to the lim  x-1-lnx / (lnx) (x-1)

                             x->1  

You can now apply L'Hopitals rule since its in the form 0/0. Remember you can only apply l'Hopitals rule if its in the form of 0/0 or ∞/∞.

 

lim     1-(1/x)            =  lim 1-(1/x) = lim      (1/x^2) 

         lnx+(x-1) (1/x)    lnx+1-(1/x)            (1/x)+(1/x^2)

Use L'Hopitals Rule again 

 

lim         1    - 1     = 1

  x->1    lnx   (x-1)   2

 

Example 3: Indeterminate Form 0⁰

 

lim (sinx)^x

  x->0+ 

y= lim (sinx)^x

  x->0+ 

lny= ln [lim(sinx)^x ]

              x->o+

lim ln(sinx)^x

    x-> 0+

 

lim xln(sinx)      

    x->0+

 

 lim       ln(sinx)      NOW USE L'Hopital's Rule

   x->0+     ( 1/x)

 

  lim    -x^2      NOW USE L'Hopitals Rule AGAIN

x->0+     cot x

 

lim     -2x/[(sec x)^2] =0

  x->0+    The answer is not ZERO. CAUTION: Remember the lny in the beginning of the problem.                                            MANY   people forget the lny

   

 

lny=0 raise it to the e on both sides to eliminate lny 

y=e^0 

Final answer the lim (sinx)^x=1

                            x->0+

 

Example 4: Indeterminate Form of the Type 0 times infinity 

 

       Indeterminate forms of the type can sometimes be evaluated by rewriting the

       product as a quotient, and then applying L’Hospital’s Rule for the indeterminate

       forms of type zero over zero or infinity over infinity 

 

            

 .

 

 

 

Proof:

 

Suppose that f and g are continuous and differentiable at c, that f(c) = g(c) = 0, and that g′(c) ≠ 0. Then